[Machine Learning and Artificial Intelligence] ANN과 MLP(Multi-layer perceptron)

이제 딥러닝의 motivate가 되는 ANN부터 개념정리 시작!

 

인공 신경망 (Aritificial Neural Networks, ANNs)이란?

생물학적 신경망을 본뜬 컴퓨팅 시스템으로, 데이터 처리 및 학습 능력을 통해 다양한 문제를 해결할 수 있도록 설계된 모델이다. ANNs는 인간의 뇌가 정보를 처리하는 방식을 모방하여, 입력 데이터를 기반으로 패턴을 학습하고 예측하는 데 사용된다

 

ANN에는 우리가 전에 알고 있던 퍼셉트론과는 달리 muti-layer perceptron을 사용한다.

간단하게 복습을 해보자

 

perceptron이란?

퍼셉트론이란? (퍼셉트론은 다수의 트레이닝 데이터를 이용하여 일종의 지도 학습을 수행하는 알고리즘)

퍼셉트론에서 결과값을 내놓는 부분은 결국 활성 함수인데, 단층 퍼셉트론에서는 이 활성 함수가 1개밖에 없는 구조이다. 인공신경망인 단층 퍼셉트론은 그 한계가 있는데, 비선형적으로 분리되는 데이터에 대해서는 제대로 된 학습이 불가능하다는 것이다.

 

그렇다면 muti-layer perceptron이 나온 이유는?

이를 극복하기 위한 방안으로 입력층과 출력층 사이에 하나 이상의 중간층을 두어 비선형적으로 분리되는 데이터에 대해서도 학습이 가능하도록 다층 퍼셉트론이 고안되었다. 입력층과 출력층 사이에 여러개의 은닉층이 있는 인공 신경망을 심층 신경망이라 부르며,  심층 신경망을 학습하기 위해 고안된 특별한 알고리즘들을 딥러닝이라고 부른다.

 

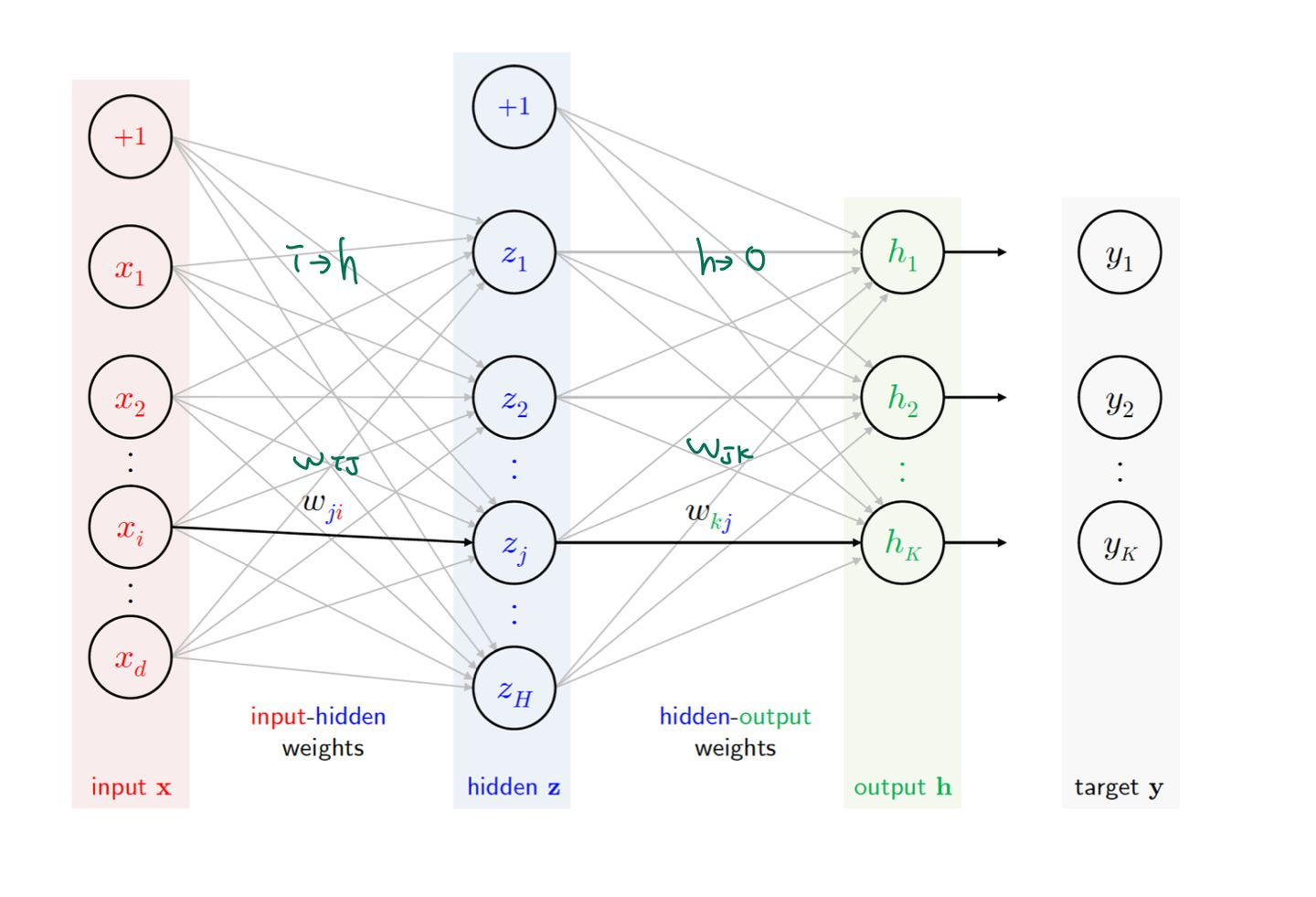
다층 퍼셉트론(Multilayer Perceptrons, MLP)은 가장 기본적인 형태의 인공 신경망이다.

MLP는 입력층(Input Layer), 하나 이상의 은닉층(Hidden Layers), 출력층(Output Layer)으로 구성된다.

각 뉴런은 활성화 함수(Activation Function)를 통해 입력 신호를 처리하고, 다음 층으로 전달한다.

 

 

 

---

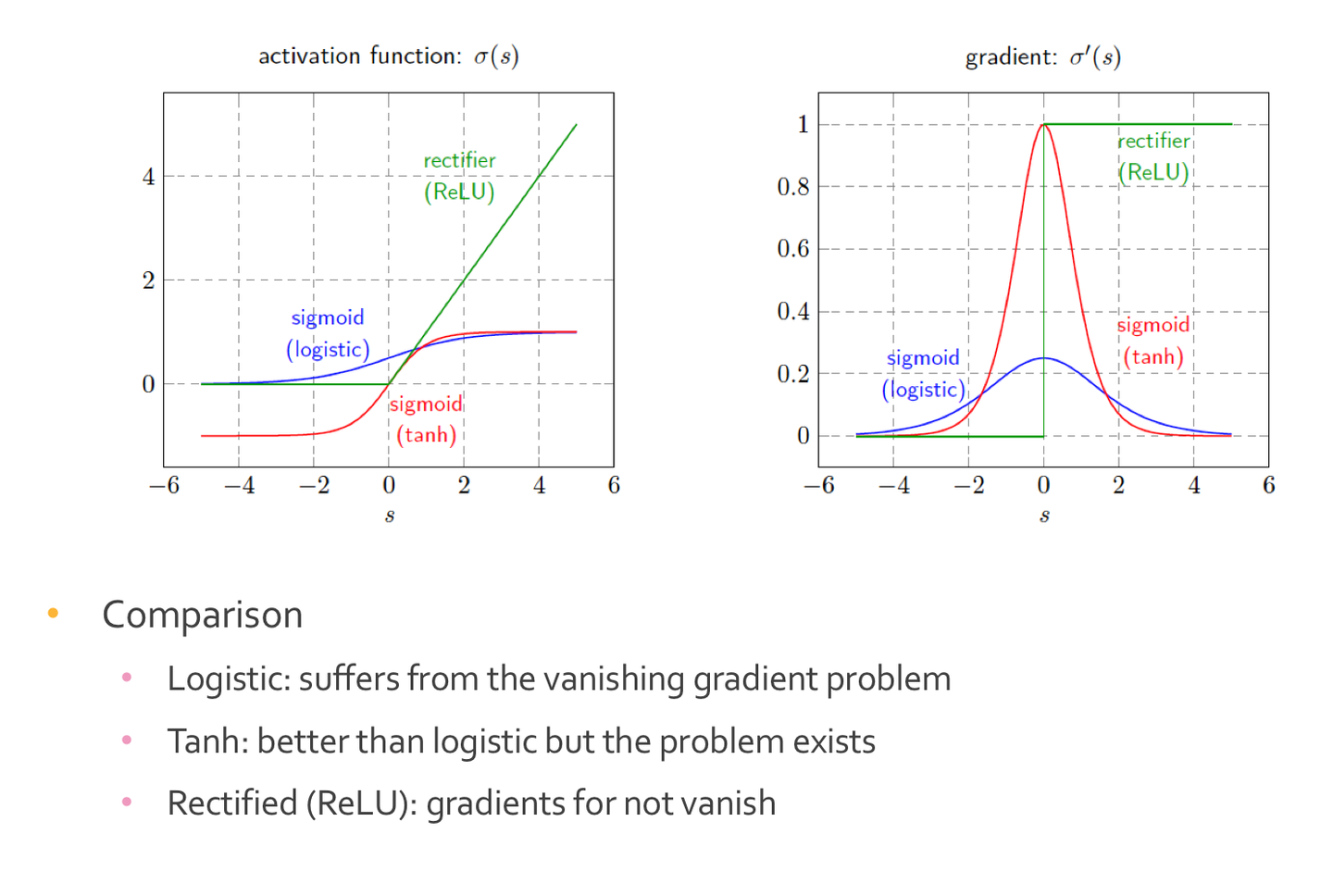
Rectifier Linear Unit (ReLU) 활성화 함수

ReLU(x)=max(0,x) 즉, 입력 값 x가 0보다 크면 그대로 출력하고, 0보다 작거나 같으면 0을 출력한다.

ReLU

 

 

특징 및 장점

1. 비선형성: 입력 값이 0보다 크면 선형적인 값을 출력하지만, 전체적으로 비선형성을 도입하여 신경망이 복잡한 패턴을 학습할 수 있게 한다.
2. 희소성: ReLU는 입력 값이 0보다 작으면 출력을 0으로 만드므로, 많은 뉴런이 0을 출력하게 된다. 이는 신경망의 희소성을 증가시켜 계산 효율성을 높이고, 과적합을 방지하는 데 도움이 된다
3. 기울기 소실 문제(Vanishing Gradient Problem)의 완화: sigmoid나 탄젠트 하이퍼볼릭 같은 함수는 입력 값이 극단적일 때 기울기가 매우 작아지는 기울기 소실 문제를 겪는다. ReLU는 입력 값이 양수인 경우 기울기가 1로 일정하게 유지되어 기울기 소실 문제를 완화한다.
4. 계산 효율성: 매우 간단한 연산 (max⁡(0,x))으로 구성되어 있어 계산 속도가 빠르고 구현이 용이하다.

단점

1. 죽은 ReLU(Dying ReLU) 문제: 학습 도중 큰 음수 입력 값이 자주 발생하면, 뉴런이 계속 0을 출력하게 되어 학습이 멈추는 현상이 발생할 수 있다.
2. 출력의 무한 범위: 렐루는 양수 입력 값에 대해 출력을 제한하지 않으므로, 큰 값이 계속 증가할 수 있다

변형

 

• Leaky ReLU: 죽은 렐루 문제를 해결하기 위해 Leaky ReLU는 음수 입력 값에 대해 작은 기울기를 허용한다.

Leaky ReLu

 

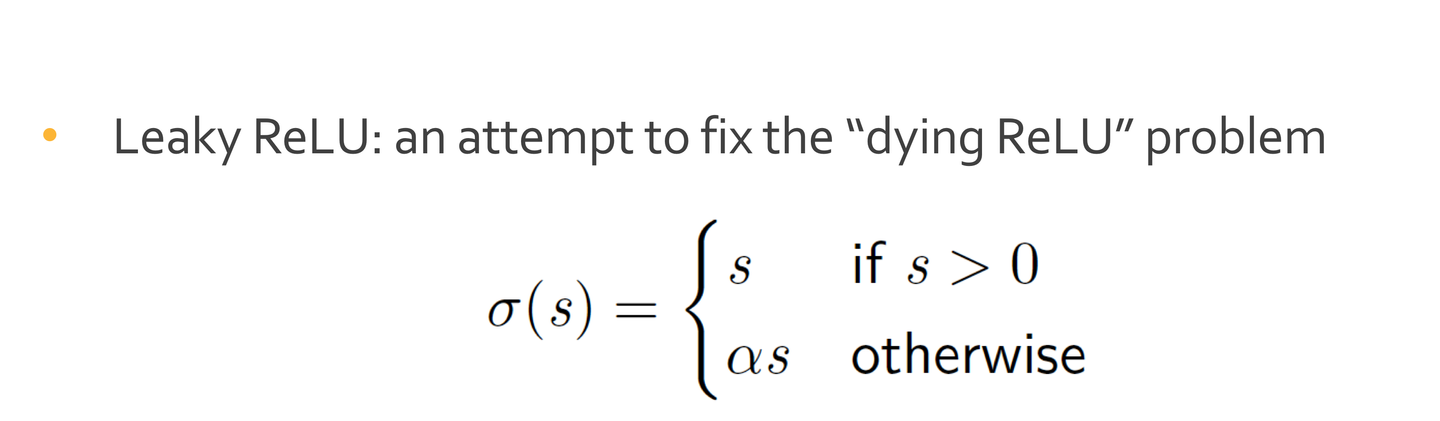
• Parametric ReLU: Leaky ReLU의 일반화로, 음수 부분의 기울기 α를 학습 가능한 매개변수로 만든다
• Exponential Linear Unit: 렐루와 유사하지만, 입력값이 음수일 때 지수 함수를 적용하여 출력이 음수 방향으로도 확장되도록 한다
• Maxout: ReLU와 달리 선형 함수의 최댓값을 취하는 형태이다.

 

---

Network Architecures

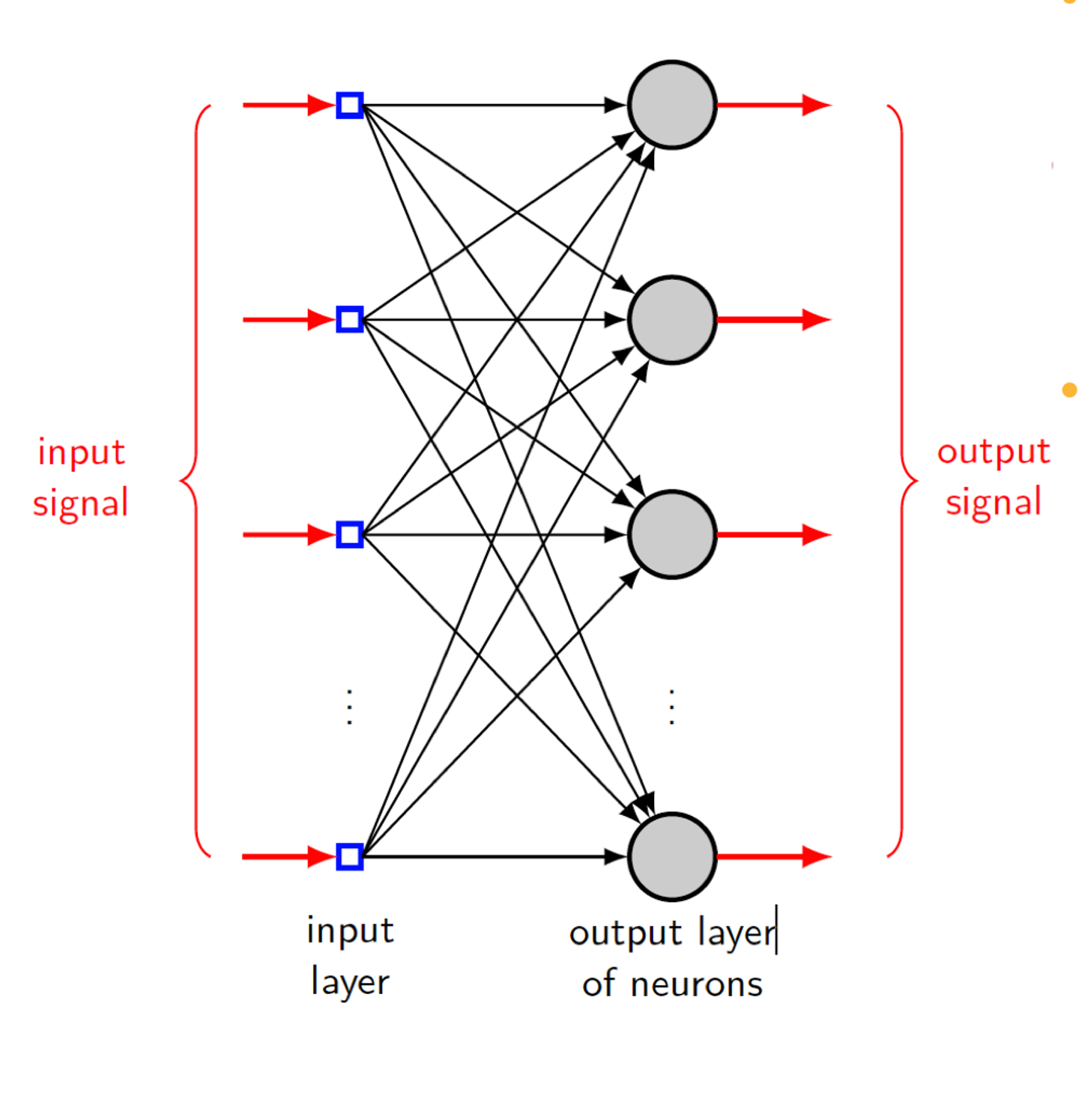
Single-later Feedforward Network

단층 전방향 신경망은 입력층과 출력층으로만 구성된 가장 단순한 현태의 신경망이다. 이 신경망에는 은닉층이 존재하지 않는다.

 

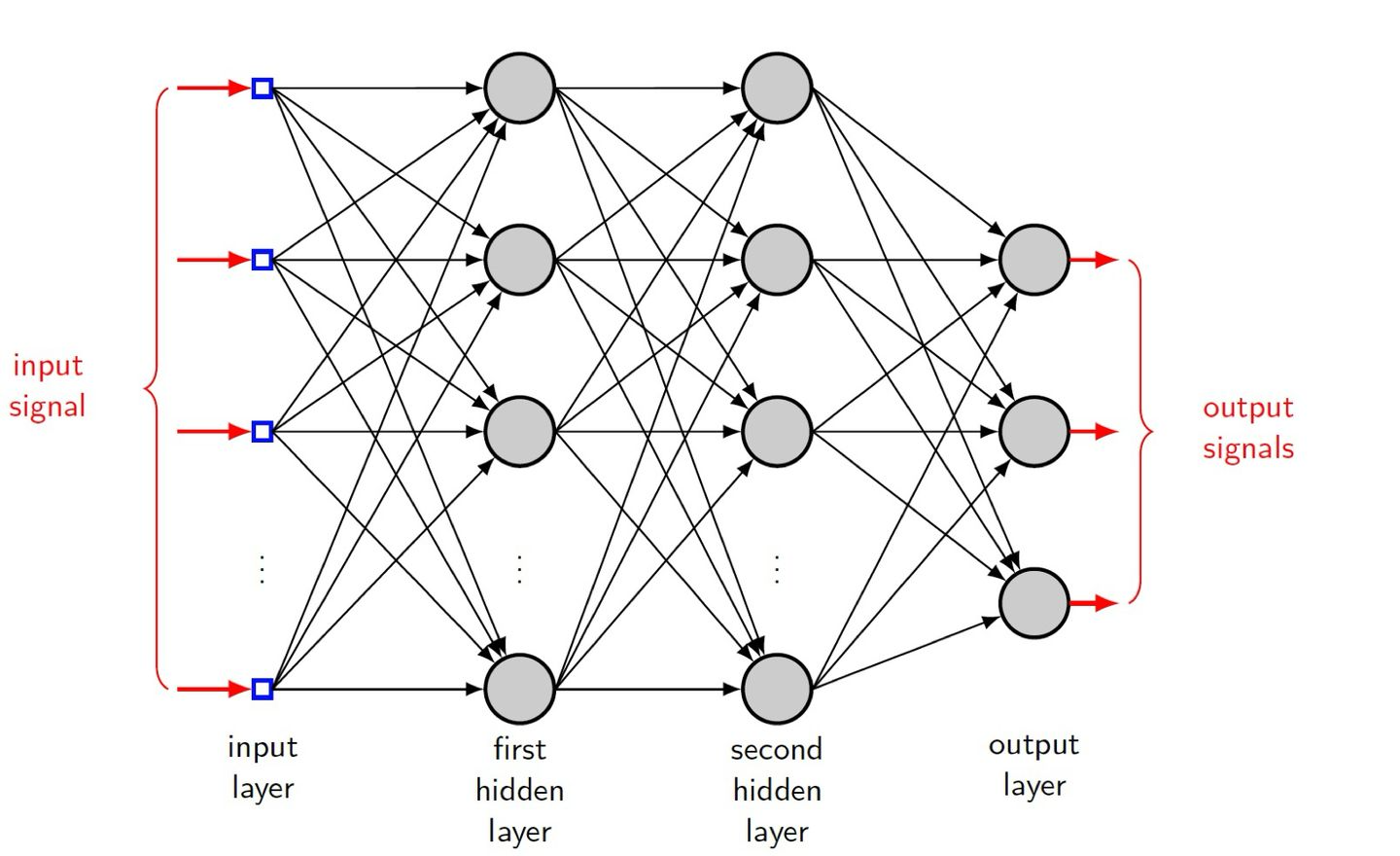
Multilayer Feedward Network

다층 전방향 신경망은 입력층과 출력층 사이에 하나 이상의 hidden layer을 포함하는 구조이다. 이러한 은닉층 덕분에 네트워크는 비선형성을 학습하고 더 복잡한 문제를 해결할 수 있다.

 

 

Function on hidden neurons

hidden neurons은 인공 신경망에서 입력층과 출력층 사이에 위치한 뉴런들로 구성된 은닉층에 속해 있다.

이 은닉 뉴런들은 신경망이 입력 데이터의 복잡한 패턴과 특징을 학습하는 데 중요한 역할을 한다.

 

---

Training Multilayer Perceptrons

MLP를 학습시키는 과정은 주로 경사 하강법(Gradient Descent)과 역전파 알고리즘(Backpropagation)을 통해 이루어진다.

학습 과정은 다음 단계로 구성된다.

1. Forward Propagation: 입력 데이터를 신경망에 통과시켜 출력 값을 계산한다.
2. Loss Calculation: 예측 값과 실제 값 간의 차이를 Loss Function를 통해 계산한다.
3. Backward Propagation: 손실을 최소화하기 위해 각 가중치와 바이어스의 기울기를 계산하고, 이를 사용하여 매개변수를 업데이트한다.

 

function signals: (forward propagation)

• 전방향 전파는 신경망이 입력 데이터를 받아 출력 값을 계산하는 과정이다. 입력층부터 시작해서 출력층까지 각 층의 뉴런들이 순차적으로 활성화되어 최종 출력이 생성된다.

 

error signals: (Backward Propagation)

• 역전파는 신경망이 예측 값과 실제 값 사이의 오차를 계산하고, 이를 통해 가중치와 편향을 업데이트하여 학습하는 과정이다. 역전파는 출력층에서 입력층으로 역방향으로 진행된다.
• 오차계산, 오차 전파: 각 층에서의 오차를 이전 층으로 전파한다. 이는 가중치와 활성화 함수의 기울기를 사용하여 계산된다
• 가중치 및 편향 업데이트: 계산된 오차를 사용하여 가중치와 편향을 업데이트한다.

 

 

Learning objective

 

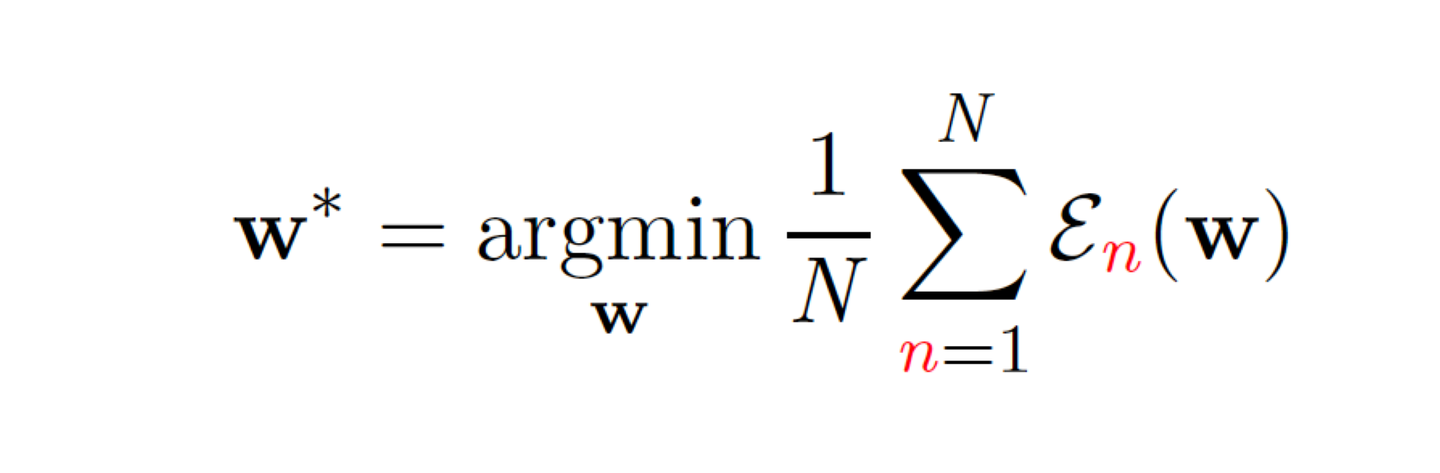
En(w): 특정 가중치 설정 w에서 n번째 샘플에 대해 계산된 손실이다.

arg⁡min⁡w: 평균 손실을 최소화하는 가중치 w를 찾는 것이 목표이다.

1. Initalization
2. Forward Propagation
3. Loss Calculation
4. Backward Propagation
5. Weight Update
6. Iteration.

 

back-propagation algorithm

인공 신경망을 훈련하는 데 사용되는 중요한 방법이다. 이 알고리즘은 출력층에서 시작하여 입력층까지 역방향으로 오차를 전파함으로써, 신경망의 가중치와 편향을 업데이트한다. 이 알고리즘은 Forward와 back으로 나뉜다

 

Forward phase: 순전파 단계에서는 입력 데이터가 신경망을 통과하며 각 층의 뉴런에서 연산을 수행하고 최종 출력 값을 생성한다

1. 입력 데이터: 입력 벡터 x가 신경망의 입력층에 전달된다
2. 계산 과정: 각 은닉층과 출력층에서 가중치와 바이어스를 사용하여 선형 변환을 수행하고, 활성화 함수를 통해 비선형을 추가한다.
3. 출력: 최종 출력층에서 예측 값 y^를 생성한다

 

Backward phase: 역전파 단계에서는 손실 함수의 기울기를 계산하여 가중치와 바이어스를 업데이트한다. 이는 출력층에서 시작하여 입력층 방향으로 진행된다.

1. 손실 함수 계산: 예측 값 y^와 실제 값 y 사이의 손실을 계산한다
2. 출력층에서의 기울기 계산
3. 은닉층에서의 기울기 계산
4. 가중치 및 bias update

 

Backward Phase (Output Layer)

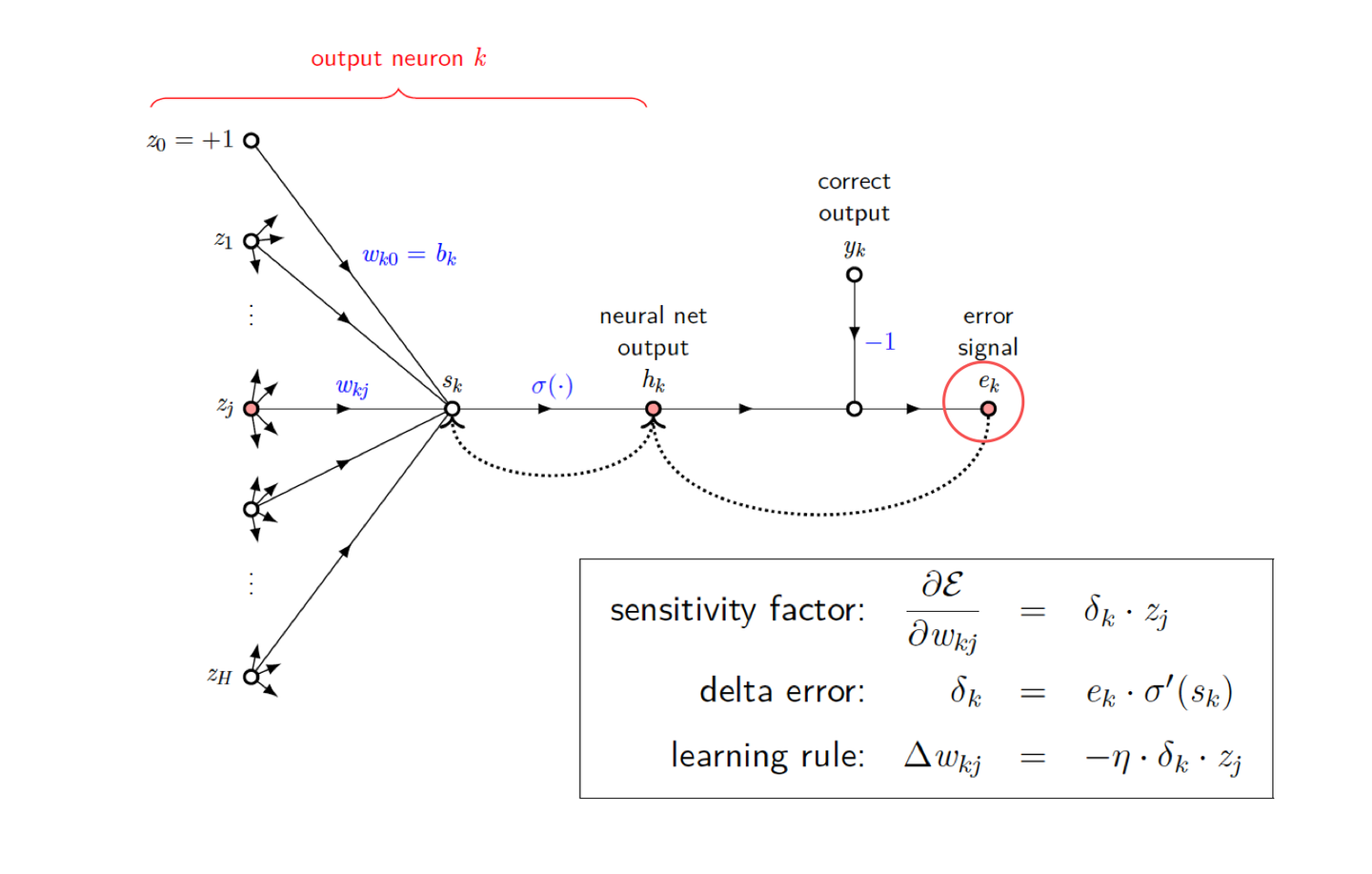
1. 오류 계산: 출력층 뉴런의 예측 값과 실제 값 간의 차이를 계산한다.
2. 델타 오류 계산: 손실 함수의 기울기와 활성화 함수의 도함수를 사용하여 델타 오류(δ\deltaδ Error)를 계산한다.
3. 가중치 및 바이어스 업데이트: 델타 오류를 기반으로 가중치와 바이어스를 업데이트한다.

 

Backward Phase (Hidden Layer)

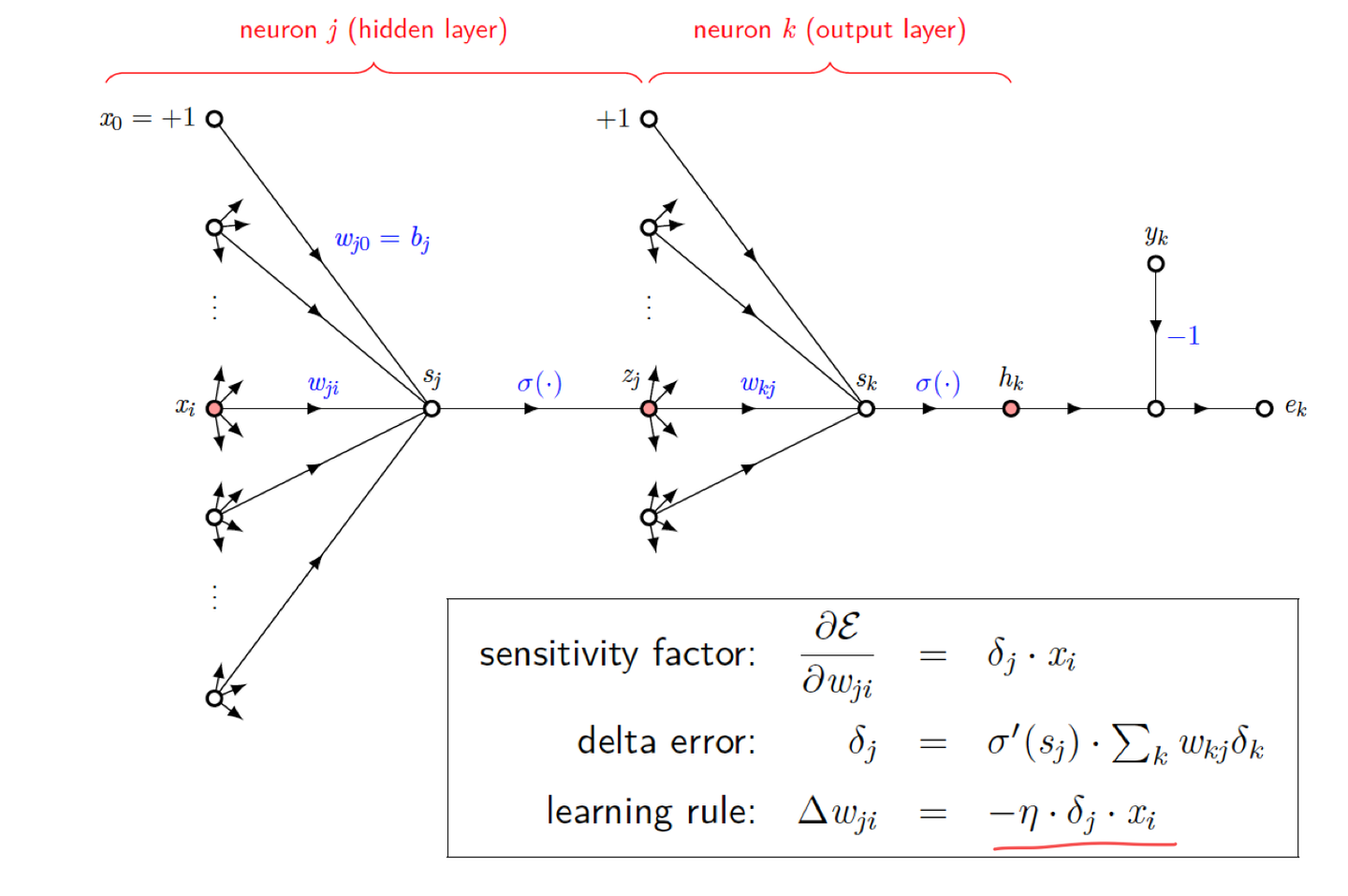
1. 오류 전파: 출력층의 델타 오류를 사용하여 은닉층의 오류를 계산한다.
2. 델타 오류 계산: 은닉층 뉴런의 기울기를 계산하여 델타 오류를 구한다.
3. 가중치 및 바이어스 업데이트: 은닉층의 가중치와 바이어스를 업데이트한다.

 

 

 

따라서 ANN이 무엇인지, ANN에 사용되는 MLP, MLP를 학습하는데 사용되는 Back-Propagation Algorithm에 알아보았다😊

 

이제는 what is the vanishing gradeint problem? 라고 묻는다면 아래와 같이 답할 수 있다.

-> It occurs when gradients become too small, hindering the learning process. Solutions such as using ReLU activations can help mitigate this problem and enable effective training of deep networks.