그래프란
그래프는 아이템들과 이들 사이의 연결 관계를 표현한다.
- vertex: 연결점, edge: 연결된 간선 의 수
그래프는 정점들의 집합과 이들을 연결하는 간선들의 집합으로 구성된 자료 구조
- V개의 정점을 가지는 무향 그래프는 최대 V*(V-1)/2 간선이 가능 ex) 5개 정점이 있는 무향 그래프의 최대 간선 수는 10 (5*4/2)개이다.
선형 자료구조나 트리 자료구조로 표현하기 어려운 N:N관계를 가지는 원소들을 표현하기에 용이하다.
그래프 유형
무향 그래프, 유향 그래프, 가중치 그래프, 사이클 없는 방향 그래프(DAG)
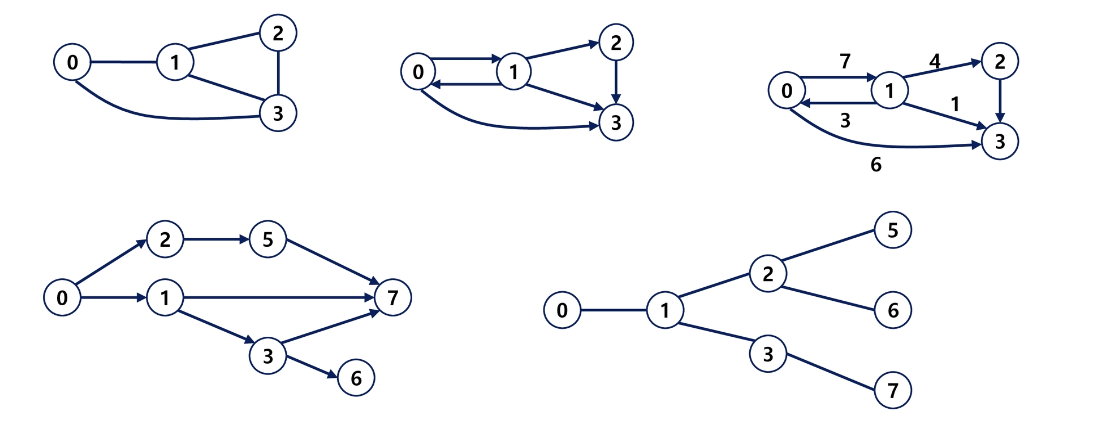
완전 그래프
- 정점들에 대해 가능한 모든 간선들을 가진 그래프
부분 그래프
- 원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
트리도 그래프이다
- 각 노드는 최대 하나의 부모 노드가 존재할 수 있다.
- 각 노드는 자식 노드가 없거나 하나 이상이 존재할 수 있다.
- 두 노드 사이에는 유일한 경로가 존재한다.
인접 정점(Adjacency)
- 두 개의 정점에 간선이 존재(연결됨_하면 서로 인접해 있다고 한다.
- 완전 그래프에 속한 임의의 두 정점들은 서로 인접해 있다.
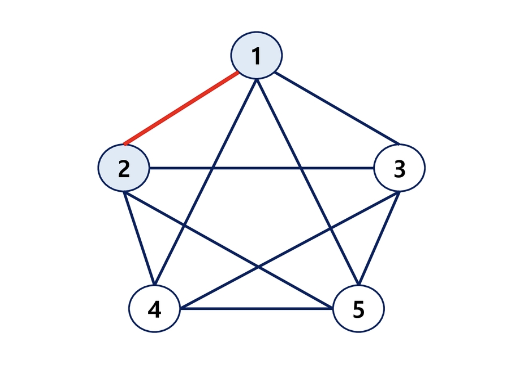
그래프 경로
- Path란 어떤 정점 A에서 시작하여 다른 정점 B로 끝나는 순회로 두 정점 사이를 잇는 간선들을 순서대로 나열한 것
- 같은 정점을 거치지 않는 간선들의 순서
- 어떤 정점에서 다른 정점으로 가는 경로는 여러가지 일 수 있다.
- Cycle: 경로의 시작 정점과 끝 정점이 같음, 시작한 정점에서 끝나는 경로
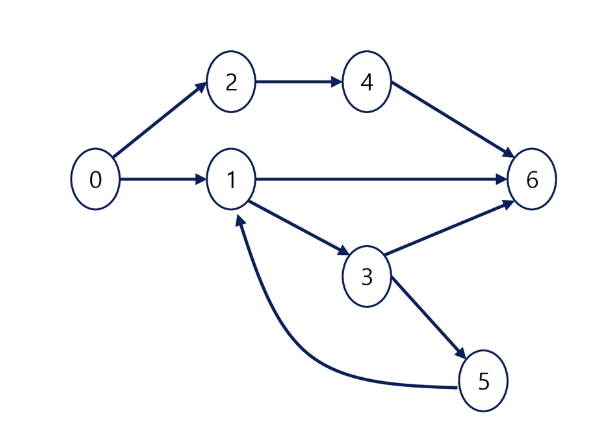
그래프 표현
- 간선의 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
- Adjacent matrix: 2차원 배열을 이용, 배열의 배열
- Adhacent List: 각 정점마다 다른 정점으로 나가는 간선의 정보를 저장
- Edge List: 간선(시작 정점, 끝 정점)의 정보를 객체로 표현하여 리스트에 저장
인접 행렬
- 두 정점을 연결하는 간선의 유무를 행렬로 표현
- V x V 정방 행렬
- 행 번호와 열 번호는 그래프의 정점에 대응
- 무향 그래프, 유향 그래프
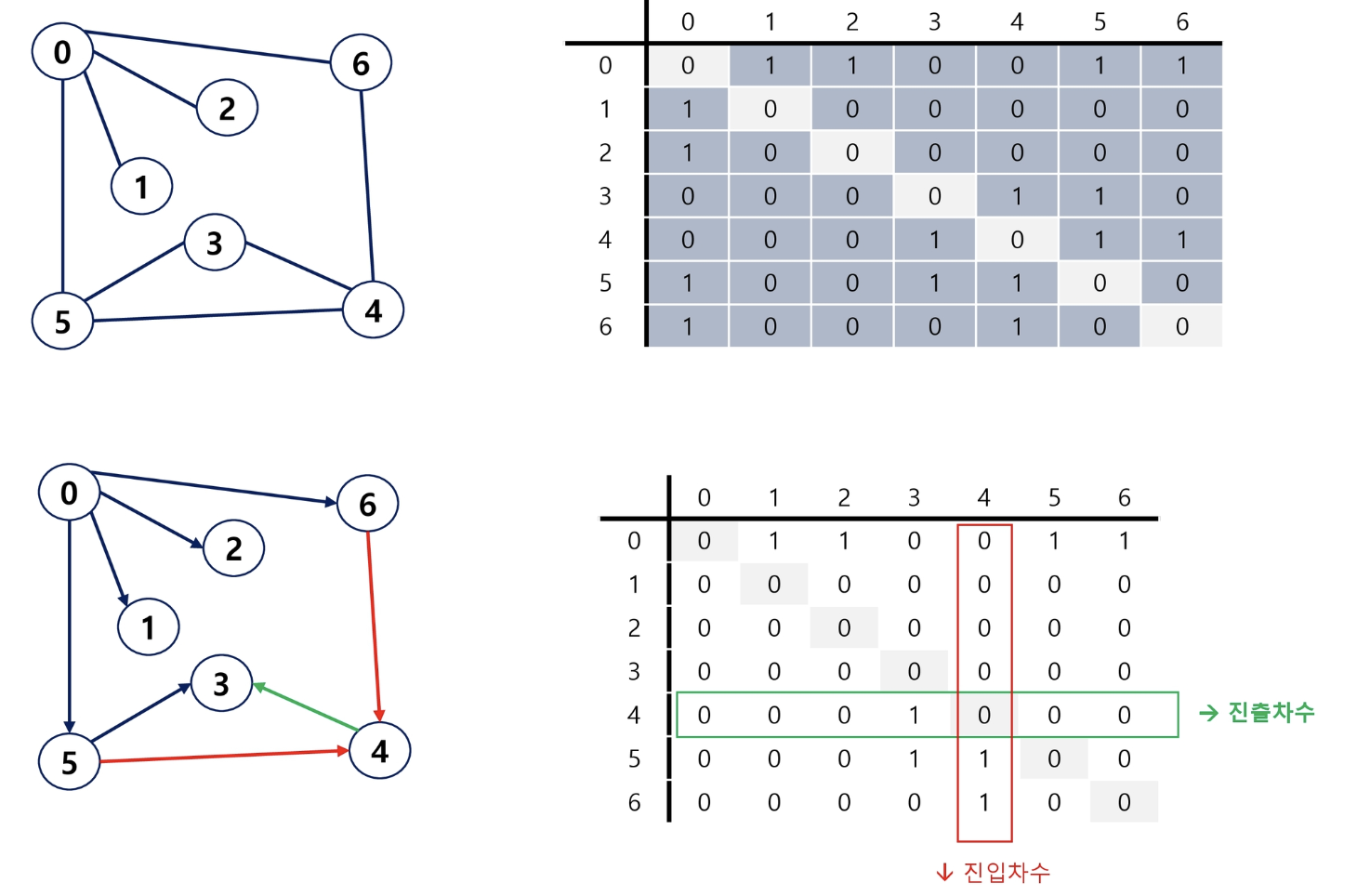
인접 행렬의 단점은?
- 메모리 비효율성
- 희소그래프에 비효율적
Sparse Graph vs Dence Graph
정점의 수에 비해 간선의 수가 매우 적다. vs 정점의 수에 미해 간선의 수가 매우 많다.
인접 리스트가 더 효율적 vs 인접 행렬이 더 효율적
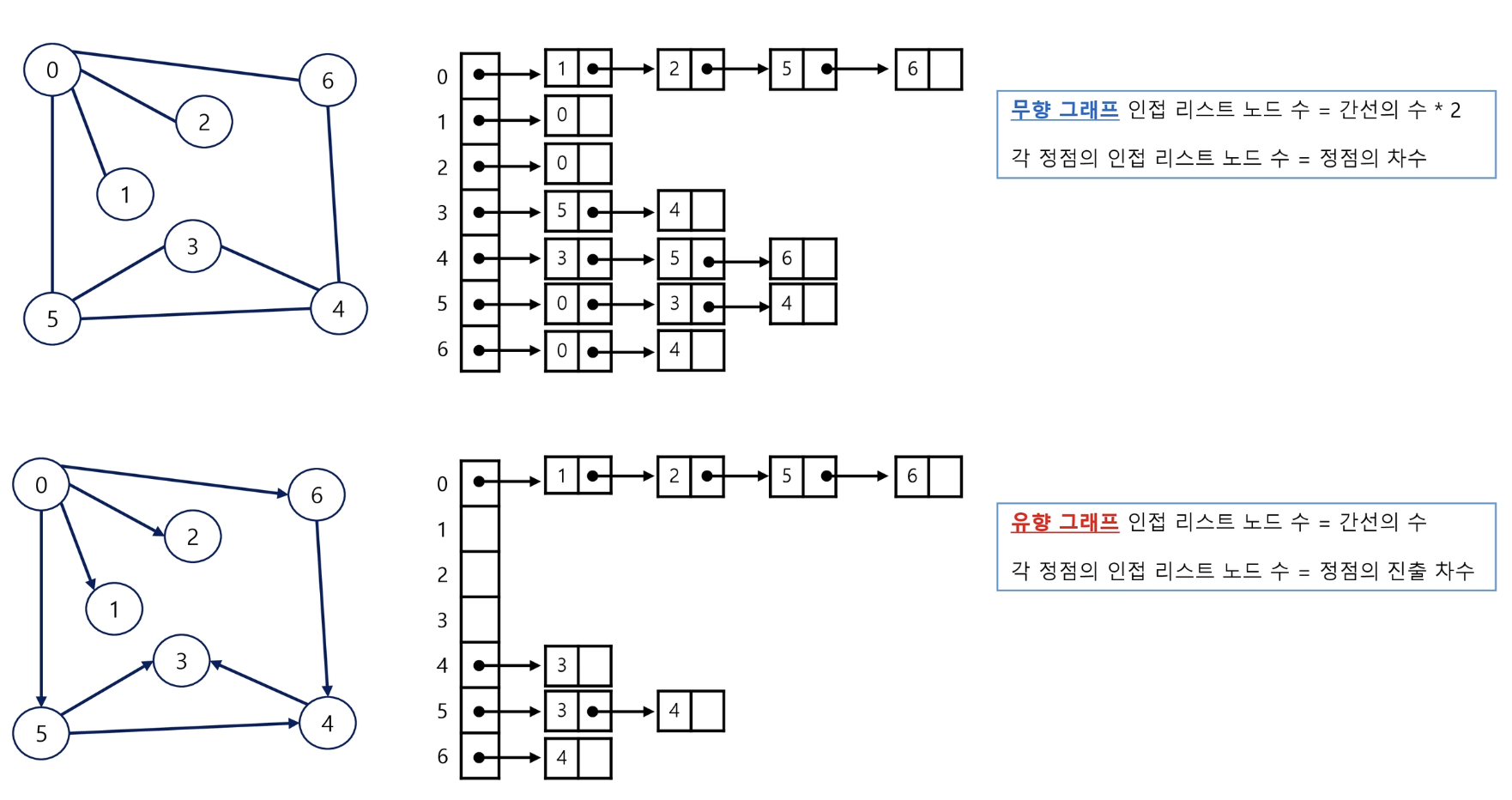
인접 리스트
- 각 정점에 대한 인접 정점들을 순차적으로 표현
- 하나의 정점에 대한 인접 정점들을 각각 노드로 하는 연결 리스트로 저장
- 무향 그래프, 유향 그래프
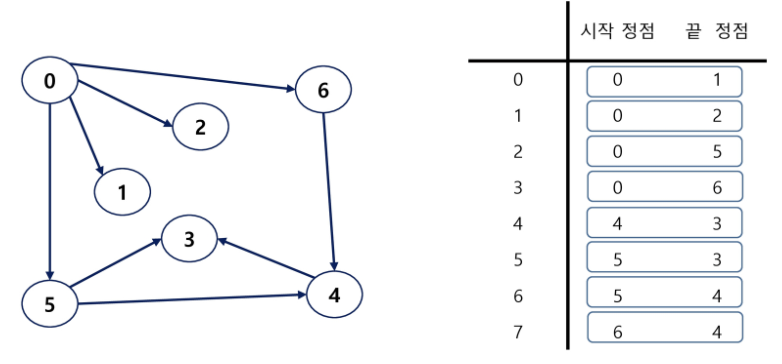
간선 리스트
- 두 정점에 대한 간선 그 자체를 객체로 표현하여 리스트로 저장
- 간선을 표현하는 두 정점의 정보를 나타냄 (시작 정점, 끝 정점)
그래프 탐색(순회)
- 그래프 순회는 비선형구조인 그래프로 표현된 모든 정점을 빠짐없이 탐색하는 것을 의미
- 너비 우선 탐색, 깊이 우선 탐색
BFS
- 너비우선탐색은 탐색 시작점의 인접한 정점들을 먼저 모두 차례로 방문한 후에, 방문했던 정점을 시작점으로 하여 다시 인접한 정점들을 차례로 방문하는 방식
- 인접한 정점들에 대해 탐색을 한 후, 차례로 다시 너비우선탐색을 진행해야 하므로, 선입선출 형태의 자료구조인 큐를 활용한다.
인접행렬로 표현
bfs(int start) {
Queue <Integer> queue = new ArrayDeque<>();
boolean[] visited = new boolean[V];
vistied[start] = true;
queue.offer(start);
while(!queue.isEmpty()) {
int cur = queue.poll();
for(int i=0; i<V; i++) {
if(adjMatrix[cur][i] == 0 || visited[i]) continue;
visited[i] = true;
que.offer(i);
}
}
}
인접 리스트로 표현
class Node{
int to;
Node next;
}
Node[] adjList;
bfs() {
adjList = new Node[V]; // V개의 정점이 있는 그래프를 나타내기 위한 인접 리스트
Queue<Integer> queue = new ArrayDeque<Integer>(); // BFS를 위한 큐
boolean visited[] = new boolean[N]; // 방문 여부를 체크하는 배열
queue.offer(start); // 시작 정점을 큐에 넣음
visited[start] = true; // 시작 정점을 방문했다고 표시
while (!queue.isEmpty()) {
int current = queue.poll(); // 큐에서 정점을 꺼냄
for (Node temp = adjList[current]; temp != null; temp = temp.next) { // 인접한 모든 정점을 탐색
if (!visited[temp.to]) {
queue.offer(temp.to); // 인접한 정점을 큐에 추가
visited[temp.to] = true; // 방문했다고 표시
}
}
}
}
Node 클래스에서
int to: 이 노드가 가리키는 정점을 나타낸다
Node next: 다음 노드를 가리키는 포인터(참조)로, LinkedList의 형태로 연결된 정점들을 관리
BFS는 최단 경로 구할시 사용!
DFS
- 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 정점으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회방법
- 가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이 우선 탬색을 반복해야 함로 재귀적으로 구현하거나 후입 선출 구조의 스택 사용
인접 행렬로 표현
private static void dfs(int current) {
visited[current] = true;
for(int i=0; i<N; ++i) {
if(adjMatrix[current][i] && !visited[i]) {
dfs(i);
}
}
}
인접 리스트로 표현
private static void dfs(int current) {
visited[current] = true;
for(Node temp = adjList[current]; temp !=null; temp=temp.next) {
if(!visited[temp.to]){
dfs(temp.to);
}
}
}
Topology Sort
- 유향 그래프의 정점들을 변의 방향을 거스르지 않도록 나열하는 것을 의미한다.
- 위상 정렬은 순서가 정해져 있는 작업들을 차례대로 수행해야 할 때, 그 순서를 결정해 주는 알고리즘이다.
- 위상 정렬을 가장 잘 설명해 줄 수 있는 예로 교육과정의 선수과목 구조를 예로 들 수 있다.
- 위상 정렬을 사용하기 위해서는 그래프가 비순환 유향 그래프(DAG)여야 한다

DFS 이용
DFS 기반 위상 정렬에서는 각 정점의 탐색을 완료했을 때 해당 정점을 스택에 추가한다.
스택에 쌓인 순서대로 정점을 나열하면 위상 정렬의 결과이다.
1. 모든 정점을 방문하지 않은 상태로 초기화한다.
2. 각 정점에 대해 DFS를 수행한다.
3. DFS 방문이 끝나면 해당 정점을 스택에 추가한다.
4. 스택에서 정점을 꺼내는 순서가 위상 정렬의 결과이다.
public class TopologySortDFS {
private static List<List<Integer>> graph = new ArrayList<>();
private static boolean[] visited;
private static Stack<Integer> stack = new Stack<>();
private static int V; //정점의 수
public static void main(String[] args) {
V = 6;
visited = new boolean[V];
for(int i=0; i<V; i++) {
graph.add(new ArrayList<>());
}
// 위상 정렬 수행
for (int i = 0; i < V; i++) {
if (!visited[i]) {
dfs(i);
}
}
// 스택에서 정점을 꺼내며 위상 정렬 결과 출력
while (!stack.isEmpty()) {
System.out.print(stack.pop() + " ");
}
}
private static void dfs(int node) {
visited[node] = true;
for(int neighbpr : graph.get(node)) {
if(!vistied[neighbor) {
dfs(neighbor);
}
}
stack.push(node);
}
}
BFS 이용
진입 차수를 이용하여 구현한다. 모든 정점의 진입 차수를 계산한 후, 집입 차수가 0인 정점을 큐에 추가한다.
큐에서 정점을 꺼내면서 해당 정점과 연결된 정점의 진입 차수를 감소시키고, 진입 차수가 0이 된 정점을 다시 큐에 추가한다.
public class TopologySortDFS {
private static List<List<Integer>> graph = new ArrayList<>();
private static boolean[] visited;
private static Stack<Integer> stack = new Stack<>();
private static int V; //정점의 수
public static void main(String[] args) {
V = 6;
indegree = new int[V];
for(int i=0; i<V; i++) {
graph.add(new ArrayList<>());
}
// 위상 정렬 수행
bfs();
}
bfs(){
Queue<Integer> que = new LinkedList<>();
List<Integer> result = new ArrayLsit<>();
//진입 차수가 0인 정점을 큐에 추가
for(int i=0; i<V; i++){
if(indegree[i]==0){
que.offer(i);
}
}
while(!que.isEmpty()) {
int current = que.poll();
result.add(current)
// 현재 정점과 연결된 모든 정점의 진입 차수를 감소
for (int neighbor : graph.get(current)) {
indegree[neighbor]--;
if (indegree[neighbor] == 0) {
queue.offer(neighbor);
}
}
}
}
}'전공 > 알고리즘' 카테고리의 다른 글
| [Kruskal, Prim 알고리즘] 서로소 집합, 최소 신장 트리 자바로 구현하기 (0) | 2024.09.01 |
|---|
그래프란
그래프는 아이템들과 이들 사이의 연결 관계를 표현한다.
- vertex: 연결점, edge: 연결된 간선 의 수
그래프는 정점들의 집합과 이들을 연결하는 간선들의 집합으로 구성된 자료 구조
- V개의 정점을 가지는 무향 그래프는 최대 V*(V-1)/2 간선이 가능 ex) 5개 정점이 있는 무향 그래프의 최대 간선 수는 10 (5*4/2)개이다.
선형 자료구조나 트리 자료구조로 표현하기 어려운 N:N관계를 가지는 원소들을 표현하기에 용이하다.
그래프 유형
무향 그래프, 유향 그래프, 가중치 그래프, 사이클 없는 방향 그래프(DAG)

완전 그래프
- 정점들에 대해 가능한 모든 간선들을 가진 그래프
부분 그래프
- 원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
트리도 그래프이다
- 각 노드는 최대 하나의 부모 노드가 존재할 수 있다.
- 각 노드는 자식 노드가 없거나 하나 이상이 존재할 수 있다.
- 두 노드 사이에는 유일한 경로가 존재한다.
인접 정점(Adjacency)
- 두 개의 정점에 간선이 존재(연결됨_하면 서로 인접해 있다고 한다.
- 완전 그래프에 속한 임의의 두 정점들은 서로 인접해 있다.

그래프 경로
- Path란 어떤 정점 A에서 시작하여 다른 정점 B로 끝나는 순회로 두 정점 사이를 잇는 간선들을 순서대로 나열한 것
- 같은 정점을 거치지 않는 간선들의 순서
- 어떤 정점에서 다른 정점으로 가는 경로는 여러가지 일 수 있다.
- Cycle: 경로의 시작 정점과 끝 정점이 같음, 시작한 정점에서 끝나는 경로

그래프 표현
- 간선의 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
- Adjacent matrix: 2차원 배열을 이용, 배열의 배열
- Adhacent List: 각 정점마다 다른 정점으로 나가는 간선의 정보를 저장
- Edge List: 간선(시작 정점, 끝 정점)의 정보를 객체로 표현하여 리스트에 저장
인접 행렬
- 두 정점을 연결하는 간선의 유무를 행렬로 표현
- V x V 정방 행렬
- 행 번호와 열 번호는 그래프의 정점에 대응
- 무향 그래프, 유향 그래프

인접 행렬의 단점은?
- 메모리 비효율성
- 희소그래프에 비효율적
Sparse Graph vs Dence Graph
정점의 수에 비해 간선의 수가 매우 적다. vs 정점의 수에 미해 간선의 수가 매우 많다.
인접 리스트가 더 효율적 vs 인접 행렬이 더 효율적
인접 리스트
- 각 정점에 대한 인접 정점들을 순차적으로 표현
- 하나의 정점에 대한 인접 정점들을 각각 노드로 하는 연결 리스트로 저장
- 무향 그래프, 유향 그래프

간선 리스트
- 두 정점에 대한 간선 그 자체를 객체로 표현하여 리스트로 저장
- 간선을 표현하는 두 정점의 정보를 나타냄 (시작 정점, 끝 정점)

그래프 탐색(순회)
- 그래프 순회는 비선형구조인 그래프로 표현된 모든 정점을 빠짐없이 탐색하는 것을 의미
- 너비 우선 탐색, 깊이 우선 탐색
BFS
- 너비우선탐색은 탐색 시작점의 인접한 정점들을 먼저 모두 차례로 방문한 후에, 방문했던 정점을 시작점으로 하여 다시 인접한 정점들을 차례로 방문하는 방식
- 인접한 정점들에 대해 탐색을 한 후, 차례로 다시 너비우선탐색을 진행해야 하므로, 선입선출 형태의 자료구조인 큐를 활용한다.
인접행렬로 표현
bfs(int start) {
Queue <Integer> queue = new ArrayDeque<>();
boolean[] visited = new boolean[V];
vistied[start] = true;
queue.offer(start);
while(!queue.isEmpty()) {
int cur = queue.poll();
for(int i=0; i<V; i++) {
if(adjMatrix[cur][i] == 0 || visited[i]) continue;
visited[i] = true;
que.offer(i);
}
}
}
인접 리스트로 표현
class Node{
int to;
Node next;
}
Node[] adjList;
bfs() {
adjList = new Node[V]; // V개의 정점이 있는 그래프를 나타내기 위한 인접 리스트
Queue<Integer> queue = new ArrayDeque<Integer>(); // BFS를 위한 큐
boolean visited[] = new boolean[N]; // 방문 여부를 체크하는 배열
queue.offer(start); // 시작 정점을 큐에 넣음
visited[start] = true; // 시작 정점을 방문했다고 표시
while (!queue.isEmpty()) {
int current = queue.poll(); // 큐에서 정점을 꺼냄
for (Node temp = adjList[current]; temp != null; temp = temp.next) { // 인접한 모든 정점을 탐색
if (!visited[temp.to]) {
queue.offer(temp.to); // 인접한 정점을 큐에 추가
visited[temp.to] = true; // 방문했다고 표시
}
}
}
}
Node 클래스에서
int to: 이 노드가 가리키는 정점을 나타낸다
Node next: 다음 노드를 가리키는 포인터(참조)로, LinkedList의 형태로 연결된 정점들을 관리
BFS는 최단 경로 구할시 사용!
DFS
- 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 정점으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회방법
- 가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이 우선 탬색을 반복해야 함로 재귀적으로 구현하거나 후입 선출 구조의 스택 사용
인접 행렬로 표현
private static void dfs(int current) {
visited[current] = true;
for(int i=0; i<N; ++i) {
if(adjMatrix[current][i] && !visited[i]) {
dfs(i);
}
}
}
인접 리스트로 표현
private static void dfs(int current) {
visited[current] = true;
for(Node temp = adjList[current]; temp !=null; temp=temp.next) {
if(!visited[temp.to]){
dfs(temp.to);
}
}
}
Topology Sort
- 유향 그래프의 정점들을 변의 방향을 거스르지 않도록 나열하는 것을 의미한다.
- 위상 정렬은 순서가 정해져 있는 작업들을 차례대로 수행해야 할 때, 그 순서를 결정해 주는 알고리즘이다.
- 위상 정렬을 가장 잘 설명해 줄 수 있는 예로 교육과정의 선수과목 구조를 예로 들 수 있다.
- 위상 정렬을 사용하기 위해서는 그래프가 비순환 유향 그래프(DAG)여야 한다

DFS 이용
DFS 기반 위상 정렬에서는 각 정점의 탐색을 완료했을 때 해당 정점을 스택에 추가한다.
스택에 쌓인 순서대로 정점을 나열하면 위상 정렬의 결과이다.
1. 모든 정점을 방문하지 않은 상태로 초기화한다.
2. 각 정점에 대해 DFS를 수행한다.
3. DFS 방문이 끝나면 해당 정점을 스택에 추가한다.
4. 스택에서 정점을 꺼내는 순서가 위상 정렬의 결과이다.
public class TopologySortDFS {
private static List<List<Integer>> graph = new ArrayList<>();
private static boolean[] visited;
private static Stack<Integer> stack = new Stack<>();
private static int V; //정점의 수
public static void main(String[] args) {
V = 6;
visited = new boolean[V];
for(int i=0; i<V; i++) {
graph.add(new ArrayList<>());
}
// 위상 정렬 수행
for (int i = 0; i < V; i++) {
if (!visited[i]) {
dfs(i);
}
}
// 스택에서 정점을 꺼내며 위상 정렬 결과 출력
while (!stack.isEmpty()) {
System.out.print(stack.pop() + " ");
}
}
private static void dfs(int node) {
visited[node] = true;
for(int neighbpr : graph.get(node)) {
if(!vistied[neighbor) {
dfs(neighbor);
}
}
stack.push(node);
}
}
BFS 이용
진입 차수를 이용하여 구현한다. 모든 정점의 진입 차수를 계산한 후, 집입 차수가 0인 정점을 큐에 추가한다.
큐에서 정점을 꺼내면서 해당 정점과 연결된 정점의 진입 차수를 감소시키고, 진입 차수가 0이 된 정점을 다시 큐에 추가한다.
public class TopologySortDFS {
private static List<List<Integer>> graph = new ArrayList<>();
private static boolean[] visited;
private static Stack<Integer> stack = new Stack<>();
private static int V; //정점의 수
public static void main(String[] args) {
V = 6;
indegree = new int[V];
for(int i=0; i<V; i++) {
graph.add(new ArrayList<>());
}
// 위상 정렬 수행
bfs();
}
bfs(){
Queue<Integer> que = new LinkedList<>();
List<Integer> result = new ArrayLsit<>();
//진입 차수가 0인 정점을 큐에 추가
for(int i=0; i<V; i++){
if(indegree[i]==0){
que.offer(i);
}
}
while(!que.isEmpty()) {
int current = que.poll();
result.add(current)
// 현재 정점과 연결된 모든 정점의 진입 차수를 감소
for (int neighbor : graph.get(current)) {
indegree[neighbor]--;
if (indegree[neighbor] == 0) {
queue.offer(neighbor);
}
}
}
}
}'전공 > 알고리즘' 카테고리의 다른 글
| [Kruskal, Prim 알고리즘] 서로소 집합, 최소 신장 트리 자바로 구현하기 (0) | 2024.09.01 |
|---|
